📢 转载信息
原文链接:https://www.qbitai.com/2025/10/339310.html
原文作者:一水
AI又又又帮数学家陶哲轩解决了一个难题!
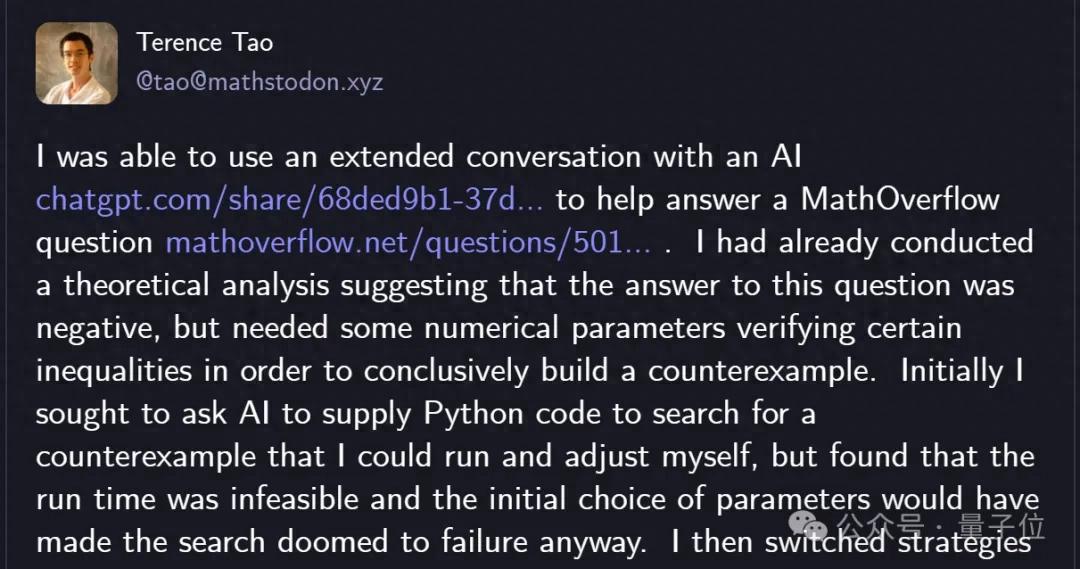
消息来自陶哲轩本人的最新发帖,他直言不讳地表示:
如果没有AI帮忙,完成同样任务就需要花费数小时(主要是手动编写代码和调试)。
甚至,如果没有AI,他也不会决定采用目前已经取得成功的关键策略。
事实上,如果没有AI帮忙,我几乎不可能尝试进行这种数值搜索(可能会寻求理论渐近分析)。
由于用的是GPT-5,OpenAI研究员Sebastien Bubeck(微软前AI副总裁&杰出科学家)也火速转发了一波,由此在社区引发热烈讨论。

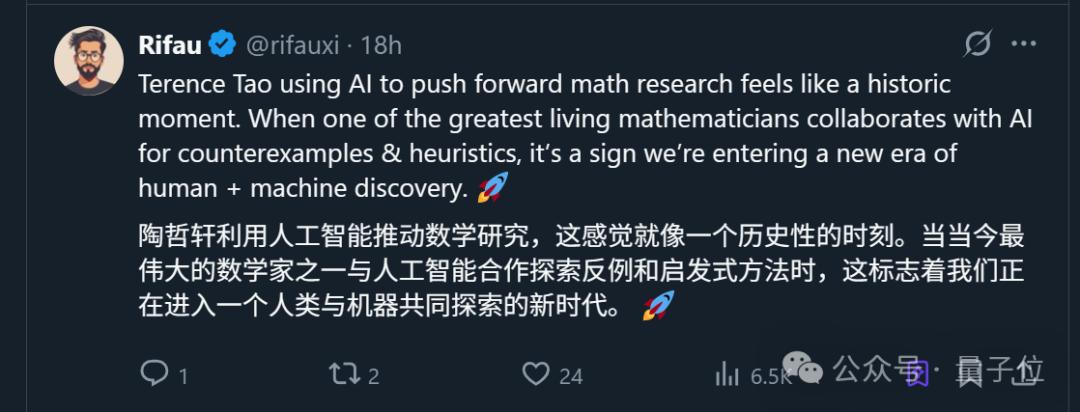
除了纷纷回忆和陶神本人类似的经历,网友们无不感慨:
这标志着我们正在进入一个人类与机器共同探索的新时代。
那么,陶哲轩这次用AI解决了什么问题?AI又在其中起了多大作用呢?
仅用29行Python代码帮助验证结果
陶哲轩这次要解决的是MathOverflow(专业数学问答社区)上的一个问题:
序列lcm(1,2,…,n)是否是高度丰数的一个子集?

简单来说,这个问题就是在比对两个特殊的数列:
一个是最小公倍数数列(lcm(1,2,…,n)),例如:
- n=2,lcm(1,2)=2
- n=3,lcm(1,2,3)=6
- n=4,lcm(1,2,3,4)=12
- n=5,lcm(1,2,3,4,5)=60
- ……
另一个是高度丰数(Highly Abundant Numbers, HA)数列。这类数的特殊性质是:其“所有约数加起来的和”,比任何比它小的数都大。
例如1的约数和是1,2的约数和是3(大于1),4的约数和是7(比3、1都大),所以它们是高度丰数。
由于前面算出来的最小公倍数们刚好也是高度丰数,所以问题来了——会不会所有的最小公倍数,永远都在高度丰数的行列里?(即子集)

对于这个问题,陶哲轩之前已经通过理论分析,得出了否定的答案。
但要完全证明这一点,还需要找到具体的数值参数来构建一个反例。这项工作需要繁琐的计算和参数搜索,人工处理需要数小时。
交给GPT-5后,一切都变得轻松了。仅通过自然语言对话和几轮沟通,AI就帮忙找到了解决方案。
起初,陶哲轩尝试让GPT-5直接生成Python程序来搜索反例参数,以便自己运行和调整。GPT-5在思考约1分19秒后,确实给出了一段较长的代码。
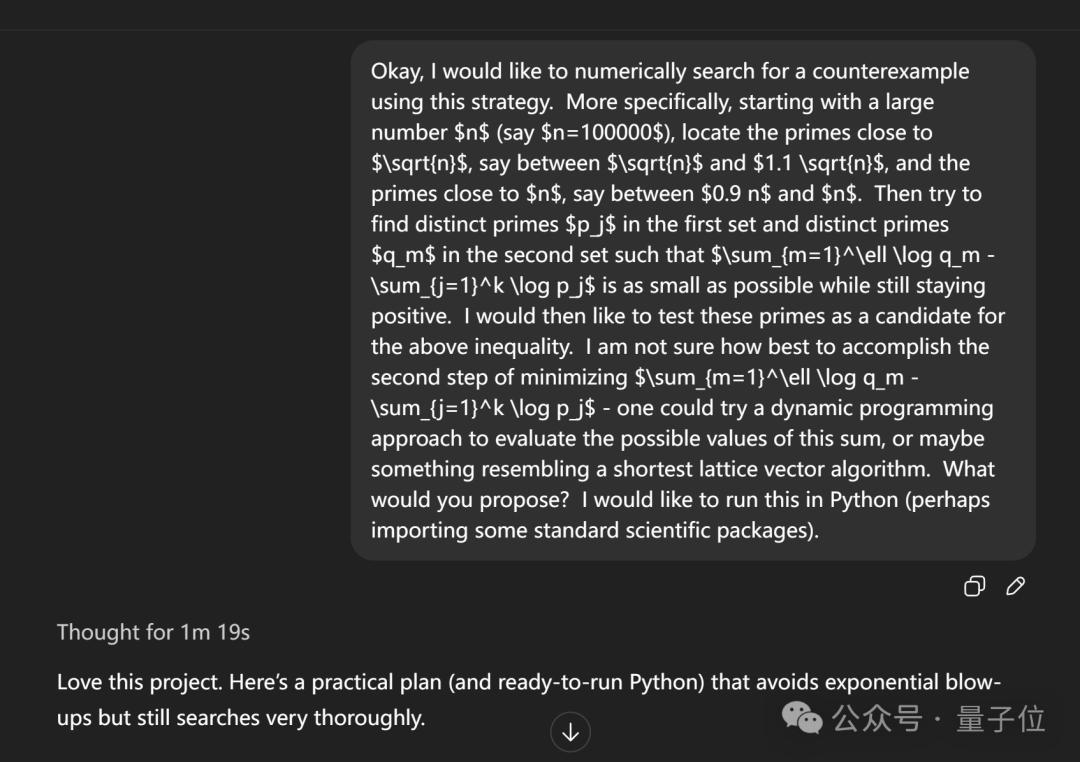
但实际运行发现,生成的代码运行时间过长,且初始参数选择不当,导致搜索失败。
于是他转变策略,通过分步对话,引导GPT-5通过启发式计算来寻找可行的参数选项。通过将大问题拆解为小问题,并在陶哲轩的指导下,GPT-5最终成功生成了符合要求的参数。
为了确保结果可靠,陶哲轩还使用了GPT-5生成的拥有29行代码的Python脚本进行独立验证。他认为这个脚本简洁明了,易于人工检查,且验证的数值结果与之前的启发式预测完全吻合。
from math import log
n = 200000; #p_j are the first 25 consecutive primes starting at 1.05*sqrt(n)
p = [ 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641 ] #q_m found by the search (13 primes)
q = [ 187963, 187973, 187987, 188011, 188017, 188021, 188029, 188299, 199931, 199933, 199961, 199967, 199999 ]
sum_log_p = sum(log(x) for x in p)
sum_log_q = sum(log(x) for x in q)
#Correction terms
sum_corr_p = sum(log(1.0 + 1.0/(x*(x+1))) for x in p)
sum_corr_q = sum(log(1.0 + 1.0/x) for x in q)
gap_q_minus_p = sum_log_q - sum_log_p
rhs_budget = sum_corr_p - sum_corr_q
print(f"sum_log_q - sum_log_p = {gap_q_minus_p:.12g}")
print(f"RHS budget = {rhs_budget:.12g}")
print("Inequality (correct sign) holds?:", (gap_q_minus_p > 0) and (gap_q_minus_p < rhs_budget))
#If you wanted the opposite sign, this is what you'd be checking:
gap_p_minus_q = -gap_q_minus_p
print(f"nsum_log_p - sum_log_q = {gap_p_minus_q:.12g}")
print("Inequality (opposite sign) holds?:", (gap_p_minus_q > 0) and (gap_p_minus_q < rhs_budget))综上,通过使用GPT-5,陶哲轩最终完成了上述问题的否定证明。
而且他还特意提到,面对数学这类严肃课题,AI这次竟然也没有犯幻觉这个“老毛病”。
我没有遇到幻觉或其他AI生成的胡言乱语的问题。

不只是这一次:陶哲轩与AI的紧密合作
事实上,作为顶尖数学大佬,这不是陶哲轩第一次用AI解决数学问题。光是今年,量子位此前就有多篇介绍:
- 9月初,他将GPT-5用于半自动化文献检索,使Erdos问题/OEIS关联项目首次得到概念验证;
- 5月下旬,新人博主陶哲轩在油管手把手演示如何只用GitHub Copilot证明函数极限问题;
- 5月中旬,油管首秀用AI 33分钟“盲证”Magma方程E1689蕴含E2;
- 3月中旬,o3-mini一眼识破并纠正了他的一个错误,然后在它的帮助下快速完成了一道数学题的解答;
- ……
在陶哲轩看来,“人工智能或许短期内不会获得菲尔兹奖(数学界的诺贝尔奖),但它或许可以充当数学家进行证明的中介”。
当然,跳出数学领域,陶哲轩的打样无疑也在告诉我们:如何用AI,相当关键。
One More Thing:关于GPT-5的最新动态
关于GPT-5,OpenAI CEO奥特曼的最新表态正在引起热议。
GPT-5被误解了!
一改往日高调姿态,他这次直接告诉大家,GPT-5代表的是迭代改进,而非突然的范式转变。也就是说,人们对GPT-5的预期过高了(也借此回应GPT-5直播出故障以及人们关于模型能力未达预期的抱怨)。
而且面对“何时实现AGI”这一问题,其态度同样来了个大转弯——相比以前直接说AGI 2030年前会实现,他这次变得更加谨慎,开始强调自己更关注安全和渐进式进步。
🚀 想要体验更好更全面的AI调用?
欢迎使用青云聚合API,约为官网价格的十分之一,支持300+全球最新模型,以及全球各种生图生视频模型,无需翻墙高速稳定,小白也可以简单操作。

评论区