📢 转载信息
原文链接:https://machinelearningmastery.com/k-means-cluster-evaluation-with-silhouette-analysis/
原文作者:Iván Palomares Carrascosa
在本文中,您将学习如何使用轮廓分析(silhouette analysis)来评估 K-Means 聚类结果,并解读平均分数和每个簇的分数,以指导模型选择。
我们将涵盖的主题包括:
- 轮廓分数衡量什么以及如何计算它
- 如何使用轮廓分析来挑选一个合理的簇数量
- 可视化每个样本的轮廓图以诊断簇的质量
以下是具体操作方法。
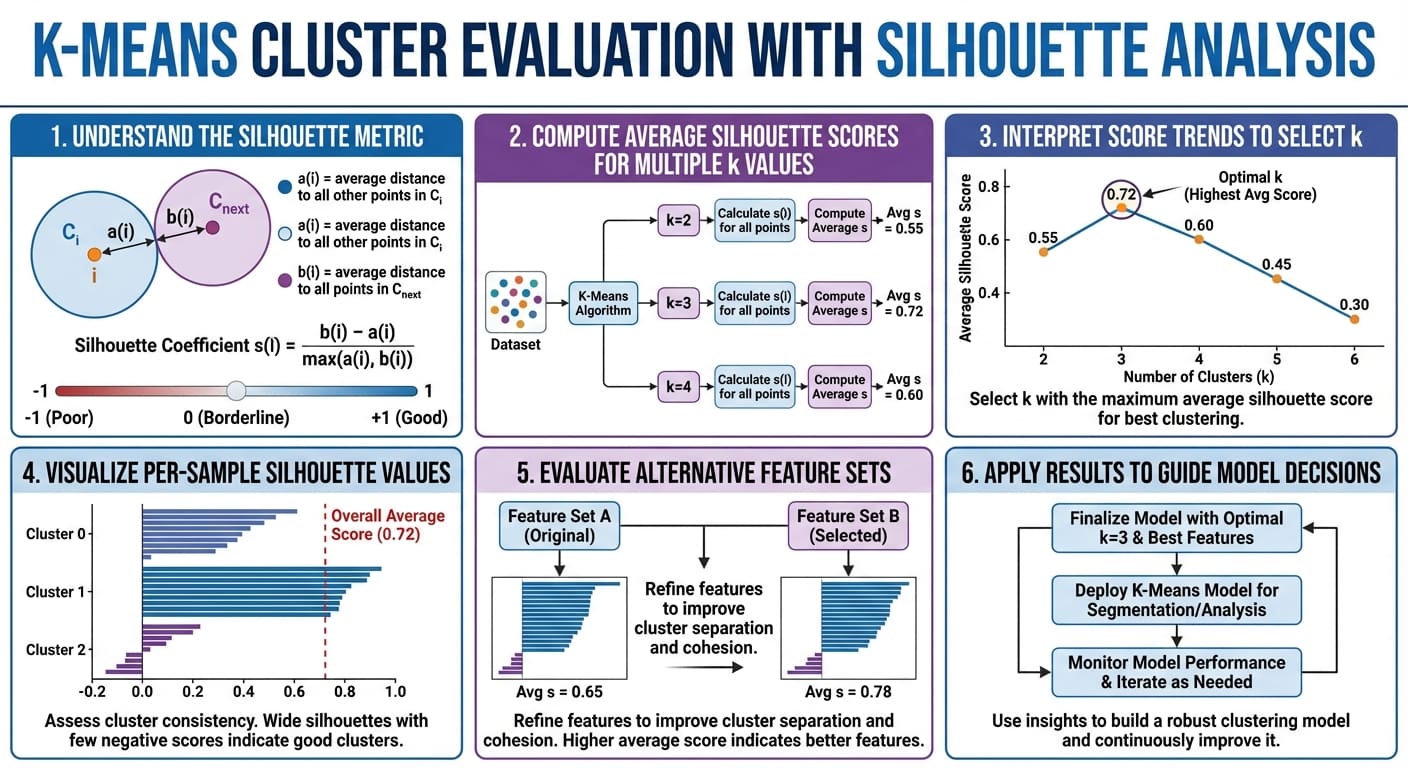
K-Means 聚类评估与轮廓分析
图片来源:Editor
引言
机器学习中的聚类模型必须通过它们将数据分离成具有明显特征的有意义组的有效性来评估。对于像 K-Means 这样的迭代算法产生的簇的内部凝聚力和相互分离性进行评估的关键指标之一就是轮廓分数(silhouette score)。该分数量化了一个对象——数据实例 i——与其自身簇的相似程度与其他簇的比较情况。
本文重点介绍如何通过轮廓分析(即基于对轮廓度量的严谨使用来分析簇的结构和有效性)来评估和解释簇的质量。轮廓分析在营销、制药、化学工程等领域的实际分割任务中具有实际意义。
理解轮廓度量
给定一个已被划分成 k 个簇的数据点或实例 i,其轮廓分数定义为:
\[ s(i) = \frac{b(i) – a(i)}{\max\{a(i), b(i)\} } \]
在公式中,a(i) 是簇内凝聚力,即 i 与其所属簇中其余点之间的平均距离。而 b(i) 是簇间分离性,即 i 与最近相邻簇中的点之间的平均距离。
轮廓分数范围从 −1 到 1。较低的 a(i) 和较高的 b(i) 值有助于获得较高的轮廓分数,这被解释为更高质量的聚类,即点与其簇紧密相关且与其他簇明显分离。总之,分数越高越好。
在实践中,我们通常计算所有实例的平均轮廓分数,以总结给定解决方案的簇质量。
轮廓分数因其同时捕获了凝聚力和分离性,被广泛用于评估不同数据集和领域的簇质量。它也是一种有用的方法,可以作为 Elbow 方法的替代或补充,用于选择适当的簇数量 k——这是应用 K-Means 及其变体等迭代方法时必需的步骤。
此外,当您绘制单个簇和簇级别的轮廓图时,轮廓分数还可以作为有见地的可视化辅助工具,其中条形的宽度反映了簇的大小。以下示例展示了一个被划分为三个簇的数据集中每个实例的轮廓图,通过按簇分组轮廓图以便与该聚类解决方案的整体平均轮廓进行比较:
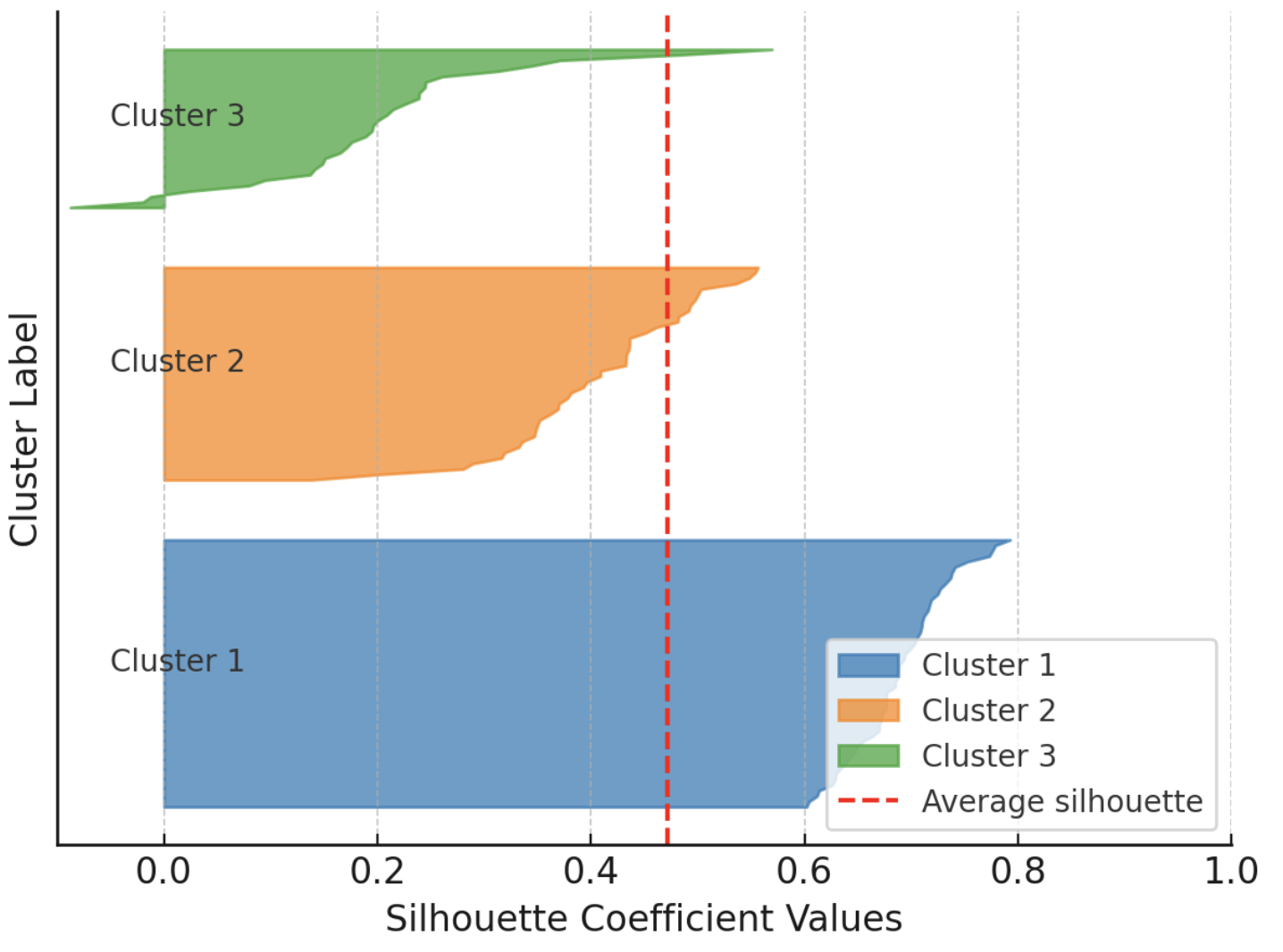
轮廓分数示例可视化
图片来源:Author
缺点是,对于某些数据集和簇形状(例如非凸形或形状复杂的簇),轮廓分析可能不太可靠,并且在非常高维的空间中可能具有挑战性。
实战轮廓分析:企鹅数据集
为了说明使用轮廓分析进行簇评估,我们将使用著名的帕尔默群岛企鹅数据集,特别是 此处可免费获取的版本。
我们快速浏览准备步骤(加载和预处理),这些步骤在 这篇聚类分析入门教程中有详细解释。我们将使用 pandas、scikit-learn、Matplotlib 和 NumPy。
import pandas as pd from sklearn.preprocessing import StandardScaler from sklearn.cluster import KMeans from sklearn.metrics import silhouette_score, silhouette_samples import matplotlib.pyplot as plt import numpy as np # Load dataset (replace with actual path or URL) penguins = pd.read_csv('https://raw.githubusercontent.com/gakudo-ai/open-datasets/refs/heads/main/penguins.csv') penguins = penguins.dropna() features = ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g'] X = penguins[features] # Scale numerical features for more effective clustering scaler = StandardScaler() X_scaled = scaler.fit_transform(X)接下来,我们应用 K-Means 来查找数据集中的簇。我们对多个簇数量 k(n_clusters 参数)重复此过程,范围从 2 到 6。对于每种设置,我们计算轮廓分数。
range_n_clusters = list(range(2, 7)) silhouette_avgs = [] for n_clusters in range_n_clusters: kmeans = KMeans(n_clusters=n_clusters, n_init=10, random_state=42) cluster_labels = kmeans.fit_predict(X_scaled) sil_avg = silhouette_score(X_scaled, cluster_labels) silhouette_avgs.append(sil_avg) print(f"For n_clusters = {n_clusters}, average silhouette_score = {sil_avg:.3f}")输出结果如下:
For n_clusters = 2, average silhouette_score = 0.531 For n_clusters = 3, average silhouette_score = 0.446 For n_clusters = 4, average silhouette_score = 0.419 For n_clusters = 5, average silhouette_score = 0.405 For n_clusters = 6, average silhouette_score = 0.392这表明 k = 2 时获得了最高的轮廓分数。这通常表明数据点分组最一致,但并不总是与生物学或领域真相相符。
在企鹅数据集中,尽管存在三种具有不同特征的物种,但重复的 K-Means 聚类和轮廓分析表明,在所选的特征空间中,将数据划分为两组可能更一致。这可能是因为轮廓分析反映的是所选特征(此处为四个数值属性)中的几何可分离性,而不是分类标签;物种之间特征的重叠可能导致 K-Means 倾向于选择少于实际物种数量的簇。
让我们可视化所有五种配置的轮廓结果:
fig, axes = plt.subplots(1, len(range_n_clusters), figsize=(25, 5), sharey=False) for i, n_clusters in enumerate(range_n_clusters): ax = axes[i] kmeans = KMeans(n_clusters=n_clusters, n_init=10, random_state=42) labels = kmeans.fit_predict(X_scaled) sil_vals = silhouette_samples(X_scaled, labels) sil_avg = silhouette_score(X_scaled, labels) y_lower = 10 for j in range(n_clusters): ith_sil_vals = sil_vals[labels == j] ith_sil_vals.sort() size_j = ith_sil_vals.shape[0] y_upper = y_lower + size_j color = plt.cm.nipy_spectral(float(j) / n_clusters) ax.fill_betweenx(np.arange(y_lower, y_upper), 0, ith_sil_vals, facecolor=color, edgecolor=color, alpha=0.7) ax.text(-0.05, y_lower + 0.5 * size_j, str(j)) y_lower = y_upper + 10 # separation between clusters ax.set_title(f"Silhouette Plot for k = {n_clusters}") ax.axvline(x=sil_avg, color="red", linestyle="--") ax.set_xlabel("Silhouette Coefficient") if i == 0: ax.set_ylabel("Cluster Label") ax.set_xlim([-0.1, 1]) ax.set_ylim([0, len(X_scaled) + (n_clusters + 1) * 10]) plt.tight_layout() plt.show()
企鹅数据集上不同 K-Means 配置的轮廓图
图片来源:Author
一个明显的观察结果是,对于 k ≥ 4,平均轮廓分数下降到大约 0.4,而对于 k = 2 或 k = 3 则更高。
如果我们考虑一个不同(更窄)的属性子集进行聚类会怎样?例如,只考虑喙长和翼展。这只需将代码开头的特征选择语句替换为:
features = ['bill_length_mm', 'flipper_length_mm']然后重新运行其余代码。尝试在聚类之前选择不同的特征,并检查轮廓分析结果是否保持相似或是否随簇数量的选择而变化。
总结
本文提供了对聚类算法标准簇质量度量的简洁、实用的理解:轮廓分数,并展示了如何使用它来批判性地分析聚类结果。
🚀 想要体验更好更全面的AI调用?
欢迎使用青云聚合API,约为官网价格的十分之一,支持300+全球最新模型,以及全球各种生图生视频模型,无需翻墙高速稳定,文档丰富,小白也可以简单操作。


评论区